Big “Oh” notation

Big “Oh” notation

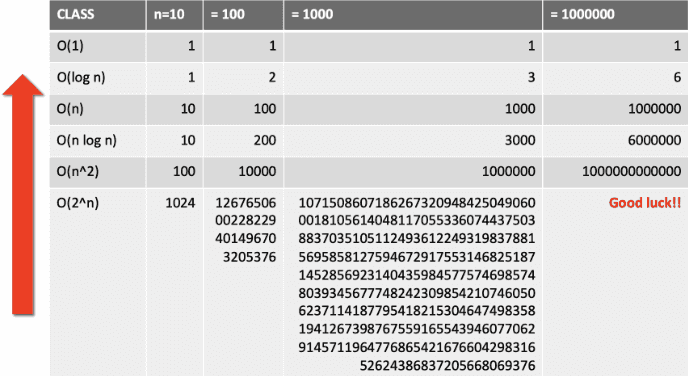
Big O notation describes the complexity of an algorithm as a function of the size of an input. How quickly an algorithm will likely run based on the number of inputs passed into it.

• performance / runtime complexity
• space complexity

Example

O(n) runtime ⇔ execution time grows linear as the input’s size. when passing input with size 5, it will take 5 times longer than input with size 1

How to compute runtime complexity

• Instructions and Conditions => O(1)

print("Hello World") => O(1)
x = 1
if 100 == 100:
print(x)

• Loops: Big O answers the question of how many times the loop body runs. O(n) with n is A.size()

sum = 0
for e in A:
sum += e

• Nested Loop: O(nxm)

for(int i = 0; i < n+10; i++) {
    for(int j = 0; j < m; j++) {
    cout<<”Hello world”<<endl;
    }
}

• Recursion: Runtime of recursion algorithm = number of recursion time runtime of each recursion. O(k1) = O(k)

public static int sum(int k) {
    if (k > 0) {
      return k + sum(k - 1);
    } else {
      return 0;
    }
}

Example

// O(logn)
def intToStr(i):
    digits = '0123456789'
    if i == 0:
        return '0'

    result = ''
    while i > 0:
        result = digits[i%10] + result
        i = i/10
    return result

def fact_recur(n):
if n <= 1:
return 1
else:
return n*fact_recur(n – 1)


O(n)

Rule

Focus on dominant term: Drop constants and multiplicative factors

• O(n^2 + 2n + 2) = O(n^2)
• O(n^3 + 100000n + 9) = O(n^3)
• O(log(n) + n + 4) = O(n)

Law of Addition

• O(f(n)) + O(g(n)) = O(f(n) + g(n))
• used with sequential statements

Law of Multiplication

• O(f(n)) O(g(n)) = O(f(n) g(n))
• used with nested statements/loops